Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
Combinatorial mathematics is a fascinating field of study that explores the relationships and patterns of combinations and permutations. Within this field, one intriguing area of research is focused on galxe polyhedra. Galxe polyhedra are three-dimensional objects consisting of interconnected polygons, presenting a rich playground for combinatorial exploration.
By investigating the combinatorial mathematics of galxe polyhedra, researchers are able to unravel the intricate connections between the various properties and characteristics of these complex structures. This exploration leads to a deeper understanding of their geometrical features, symmetries, and topological properties.
The study of galxe polyhedra provides insight into a variety of mathematical concepts, such as graph theory, symmetry groups, and polyhedral geometry. These mathematical tools help researchers not only analyze and classify different galxe polyhedra, but also establish relationships between them and other mathematical structures.
Moreover, the combinatorial exploration of galxe polyhedra has practical applications in a wide range of fields, including architecture, materials science, and computer graphics. By understanding the combinatorial properties of these complex structures, researchers can design new materials, create aesthetically pleasing architectural structures, and develop efficient algorithms for computer simulations.
Overall, investigating the combinatorial mathematics of galxe polyhedra is a captivating and multi-faceted research area that continues to push the boundaries of our mathematical knowledge. Through this exploration, we gain new insights into the fundamental principles of combinatorics and uncover the hidden beauty of these mesmerizing three-dimensional objects.
Combinatorial mathematics is a branch of mathematics that focuses on counting and organizing objects depending on certain properties and restrictions. It provides a fundamental framework for understanding and solving problems in various fields, such as computer science, cryptography, optimization, and graph theory.
At its core, combinatorial mathematics deals with the analysis of discrete structures, such as sets, permutations, combinations, graphs, and polyhedra. These structures are often studied using combinatorial techniques, which involve counting, enumeration, and arrangement of elements.
One important concept in combinatorial mathematics is that of a combinatorial object. A combinatorial object is a discrete structure that can be represented as a set of elements or as a structured arrangement of elements. Examples of combinatorial objects include permutations of a set, subsets of a set, and graphs.
Combinatorial mathematics also involves the study of combinatorial identities and combinatorial properties. Combinatorial identities are equations that relate combinatorial objects and provide a way to count or evaluate them. Combinatorial properties, on the other hand, are specific characteristics or properties that can be used to classify or describe combinatorial objects.
Understanding combinatorial mathematics is essential for solving problems that involve counting, enumeration, and arrangement of objects. It provides powerful tools and techniques that can be applied to various real-world problems, such as scheduling, network optimization, and data analysis.
Galxe's application modules serve the purpose of providing specialized tools and features for investigating the combinatorial mathematics of galxe polyhedra. These modules allow researchers and enthusiasts to explore the properties, patterns, and relationships of galxe polyhedra using combinatorial methods and algorithms.
The Galxe application modules offer a user-friendly interface for working with galxe polyhedra, providing functionalities such as generating and visualizing polyhedra, calculating their combinatorial properties, and analyzing their combinatorial structures. These modules aim to facilitate the study and understanding of galxe polyhedra, as well as to inspire new research and insights in the field of combinatorial mathematics.
In addition, the Galxe application modules also provide a platform for collaborative research and knowledge sharing among mathematicians, scientists, and enthusiasts interested in the combinatorial mathematics of galxe polyhedra. Through the exchange of ideas, algorithms, and data, these modules foster a vibrant community that contributes to the advancement of combinatorial mathematics and its applications in various domains.
1. Accessibility: The modules are designed to be accessible to both experts and beginners in combinatorial mathematics, providing an intuitive interface and clear documentation.
2. Efficiency: The modules incorporate efficient algorithms and data structures to ensure fast computations and analysis of galxe polyhedra.
3. Visualization: The modules offer interactive visualizations that aid in understanding the combinatorial structures and properties of galxe polyhedra.
4. Collaboration: The modules promote collaboration and knowledge sharing among researchers and enthusiasts through a community-driven platform.
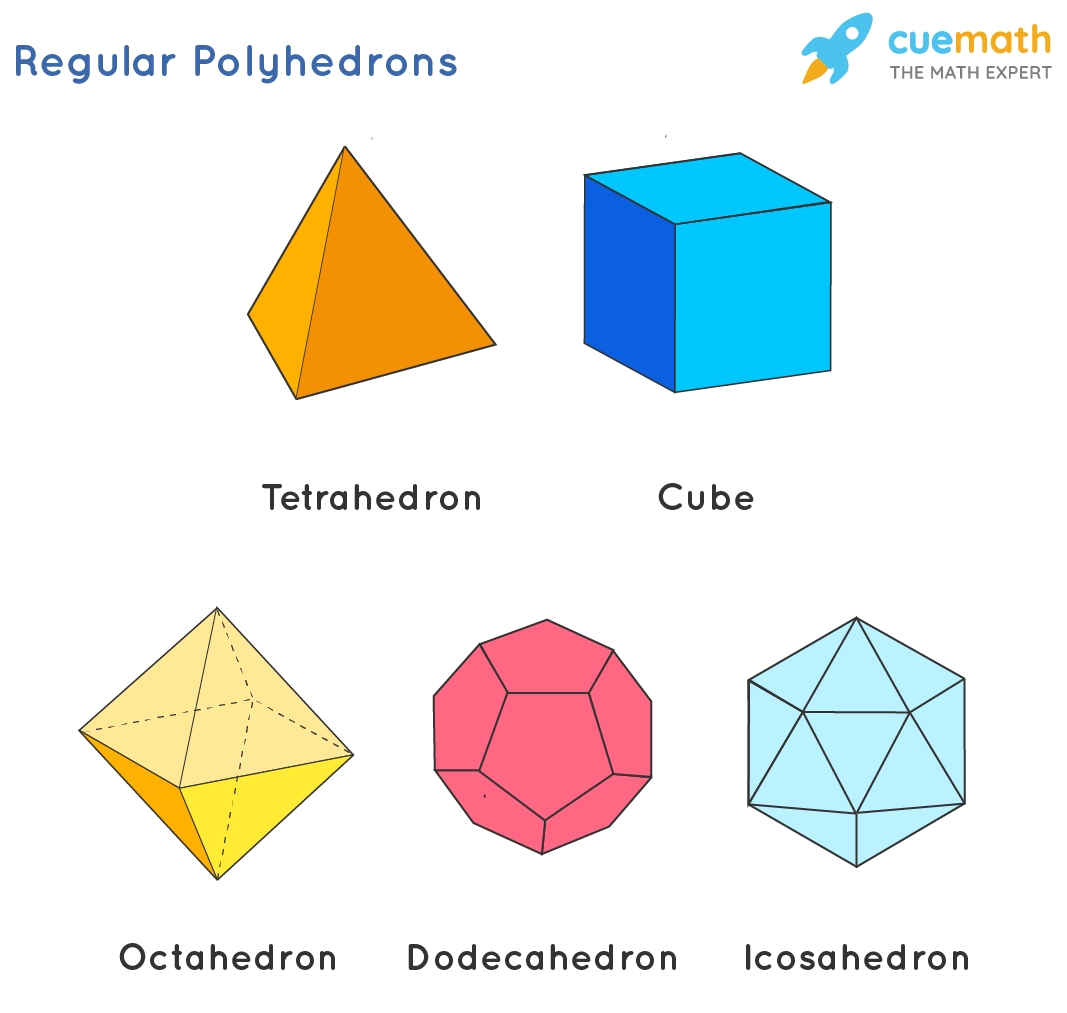
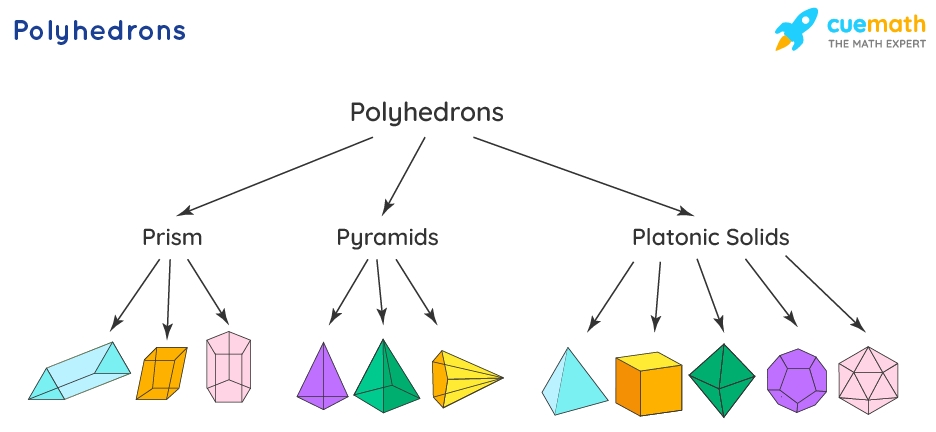
Galxe polyhedra are a fascinating area of study in combinatorial mathematics. They are three-dimensional figures built by combining regular polygons. Understanding the properties and characteristics of these polyhedra is important for various fields, including architecture, computer graphics, and materials science.
A galxe polyhedron is defined as a convex polyhedron where each face is a regular polygon and each vertex connects three or more faces. The polygons can be any regular shape, such as triangles, squares, or pentagons. The polyhedron is named after its creator, Dr. Galxe, who made significant contributions to the field of combinatorial mathematics.
Galxe polyhedra have several interesting properties that make them unique. Some of these properties include:
Edge Lengths: In a galxe polyhedron, the lengths of the edges can vary depending on the shapes and sizes of the regular polygons used to construct it.
Vertex Degree: Each vertex in a galxe polyhedron connects to three or more faces, making it a high-degree vertex.
Face Angles: The angles within each regular polygon face of a galxe polyhedron remain constant.
Galxe polyhedra have practical applications in various fields. Some common applications include:
Architecture: Galxe polyhedra can be used as interesting architectural designs, providing unique shapes and structural stability.
Computer Graphics: Galxe polyhedra can be used to create 3D models for computer graphics, gaming, and virtual reality applications.
Materials Science: Understanding the structural properties of galxe polyhedra can assist in designing new materials with specific characteristics, such as strength and flexibility.
fad8a57530f54ac885febf32a9396890
The study of combinatorial aspects of Galxe polyhedra has gained significant attention in recent years. Galxe polyhedra are a type of three-dimensional structure characterized by their unique combinatorial properties. By examining the ways in which the faces, vertices, and edges of these polyhedra combine and interact, researchers have been able to uncover fascinating insights and patterns.
One key aspect of Galxe polyhedra is their vertex arrangement. Unlike traditional polyhedra, which have a regular arrangement of vertices, Galxe polyhedra exhibit a more complex and irregular configuration. This arrangement can have a profound impact on the overall structure and properties of the polyhedra, leading to a rich array of combinatorial possibilities.
Another important aspect is the combinatorial symmetry of Galxe polyhedra. Researchers have discovered that these polyhedra often possess symmetrical properties that can be described using mathematical formulas and algorithms. This symmetry allows for a deeper understanding of the underlying combinatorial structure of Galxe polyhedra, as well as potential applications in fields such as architecture and materials science.
Furthermore, the combinatorial aspects of Galxe polyhedra play a crucial role in their classification and enumeration. By examining the possible combinations of faces, vertices, and edges, researchers can categorize Galxe polyhedra into distinct classes based on their combinatorial properties. This classification system provides a framework for organizing and studying these unique structures, allowing for a more systematic approach to their analysis.
In conclusion, the study of combinatorial aspects of Galxe polyhedra offers a fascinating insight into the world of three-dimensional structures. By exploring the vertex arrangement, combinatorial symmetry, and classification of these polyhedra, researchers can uncover hidden patterns and properties that have implications in various disciplines. This research not only deepens our understanding of combinatorial mathematics but also opens up new possibilities for practical applications.
Galxe polyhedra are a class of geometric figures that have captivated the attention of mathematicians for centuries. These polyhedra possess unique properties and exhibit intricate structures, making them fascinating objects of study.
Enumerating Galxe polyhedra involves determining the total number of distinct polyhedra within this class. This task requires combinatorial mathematics techniques as well as a thorough understanding of their defining characteristics.
Galxe polyhedra are three-dimensional solids composed of flat faces, edges, and vertices.
The faces of Galxe polyhedra are regular polygons, meaning that all sides and angles are congruent.
The number of faces meeting at each vertex of a Galxe polyhedron is the same for all vertices.
Galxe polyhedra are convex, meaning that the line segment connecting any two points on their surface lies entirely within the figure.
To enumerate Galxe polyhedra, several approaches can be employed:
Enumeration by Symmetry: Exploiting the symmetries present in Galxe polyhedra to reduce the search space and classify different configurations.
Enumeration via Generating Functions: Utilizing generating functions to count the number of distinct Galxe polyhedra based on their properties and characteristics.
Enumeration using Graph Theory: Representing Galxe polyhedra as graphs and employing graph theory techniques, such as enumeration of connected graphs or using generating functions.
Each of these approaches has its advantages and challenges, and researchers continue to explore new methods to improve the efficiency and accuracy of Galxe polyhedra enumeration.
In conclusion, the enumeration of Galxe polyhedra is a complex and intriguing field of study that combines combinatorial mathematics, symmetry, and graph theory. The diverse methods employed by mathematicians seek to unravel the secrets hidden within these mesmerizing geometric structures.
The study of galxe polyhedra involves investigating their topological properties. Topology is a branch of mathematics concerned with the properties of objects that are preserved under continuous transformations. In the context of galxe polyhedra, we are interested in understanding how these objects can be manipulated and transformed while preserving their overall structure.
One important topological property of galxe polyhedra is their connectivity. The connectivity of a polyhedron refers to the number of separate pieces it can be split into without cutting through any edges or faces. Galxe polyhedra often have high connectivity, meaning they cannot be easily separated into smaller components.
Another topological property of interest is the genus of a galxe polyhedron. The genus is a measure of the number of handles or tunnels present in the polyhedron. A polyhedron with no handles or tunnels has a genus of zero, while a polyhedron with one handle has a genus of one. The genus of a galxe polyhedron can provide insight into its overall complexity and structure.
In addition to connectivity and genus, we also consider the Euler characteristic of galxe polyhedra. The Euler characteristic is a topological invariant that describes the relationship between the number of vertices, edges, and faces of a polyhedron. For galxe polyhedra, the Euler characteristic can help us understand the overall shape and configuration of the object.
The study of topological properties in galxe polyhedra is essential for understanding their combinatorial mathematics. By examining how these objects can be transformed and manipulated while preserving their structure, we can gain valuable insights into their properties and applications in various fields, such as chemistry, physics, and computer science.
Galxe polyhedra are a fascinating area of study in combinatorial mathematics. These polyhedra have unique properties that make them especially interesting for researchers. By investigating the geometry of galxe polyhedra, we can gain a deeper understanding of their structure and how they relate to other mathematical concepts.
One aspect of galxe polyhedra that researchers often explore is their vertex configurations. A vertex configuration refers to the arrangement of vertices around a specific vertex in the polyhedron. By examining the different vertex configurations in galxe polyhedra, we can identify patterns and relationships that can help us classify and categorize these structures.
In addition to vertex configurations, the faces of galxe polyhedra also provide valuable insights into their geometry. The shapes and arrangements of faces can give us clues about the overall structure of the polyhedron, such as whether it is convex or concave, and how the faces connect to form the 3-dimensional shape.
Another important aspect to investigate is the symmetries of galxe polyhedra. Symmetry plays a crucial role in understanding the structure and properties of these polyhedra. By studying the symmetries, we can identify rotational or reflectional patterns that help us classify and analyze galxe polyhedra.
Research on the geometry of galxe polyhedra is still ongoing, and there is much more to discover. Advances in computer modeling and visualization have made it possible to explore these structures in new and exciting ways. By combining theoretical analysis with computational techniques, researchers can uncover previously unknown properties and relationships within galxe polyhedra.
In conclusion, investigating the geometry of galxe polyhedra is an important area of research in combinatorial mathematics. By examining vertex configurations, face arrangements, and symmetries, we can gain a deeper understanding of these fascinating structures. This knowledge has practical applications in various fields such as architecture and materials science, where understanding the properties of complex geometric shapes is essential.
Galxe polyhedra are a class of geometric structures that exhibit fascinating properties in their shape and structure. In this section, we explore some of the key geometric properties of these polyhedra.
1. Symmetry: Galxe polyhedra often possess high degrees of symmetry, with multiple axes of rotational symmetry and reflectional symmetry planes. This symmetry contributes to their aesthetic appeal and makes them ideal for various applications in design and architecture.
2. Vertex Configuration: The vertices of a galxe polyhedron have unique arrangements that determine the connectivity and shape of the polyhedron. The study of vertex configurations provides insights into the combinatorial properties of galxe polyhedra.
3. Face Types: The faces of galxe polyhedra can vary in shape and size. Common face types include triangles, squares, pentagons, and hexagons. Understanding the distribution and arrangement of these face types contributes to our understanding of the overall structure of galxe polyhedra.
4. Surface Curvature: Galxe polyhedra can exhibit both positive and negative surface curvature, leading to intriguing geometric properties. The study of surface curvature helps analyze the stability and behavior of these polyhedra under different conditions.
5. Intersecting Edges: Galxe polyhedra often have edges that intersect with one another, creating interesting topological configurations. The study of intersecting edges helps unravel the complex mathematical relationships between the vertices, edges, and faces of these polyhedra.
In summary, the geometric properties of galxe polyhedra encompass symmetry, vertex configuration, face types, surface curvature, and intersecting edges. Exploring these properties allows for a deeper understanding of the structure and mathematics underlying these fascinating geometric structures.
Understanding the relations between combinatorial and geometric aspects is crucial in investigating the combinatorial mathematics of galxe polyhedra. These two aspects are closely intertwined and provide valuable insights into the structure and properties of these polyhedra.
In combinatorial mathematics, the focus is on studying the combinatorial properties of galxe polyhedra, such as their vertex configurations, edge lengths, and face distributions. Combinatorial techniques, including graph theory and combinatorial optimization, are used to analyze and classify these properties.
On the other hand, geometric aspects deal with the spatial arrangement and shape of galxe polyhedra. This includes the angles between faces, dihedral angles between adjacent faces, and the overall symmetry of the polyhedra. Geometric methods, such as Euclidean geometry and differential geometry, are used to analyze and describe these aspects.
The interplay between combinatorial and geometric aspects is fundamental to understanding galxe polyhedra. On one hand, the combinatorial properties of polyhedra determine their geometric properties. For example, the vertex configuration of a polyhedron determines how its faces are connected, which in turn affects its spatial arrangement.
On the other hand, the geometric properties of polyhedra can provide insights into their combinatorial structure. For instance, the dihedral angles between adjacent faces can reveal additional symmetries and constraints on the vertex configurations and edge lengths.
The relations between combinatorial and geometric aspects have important applications in various fields. In the field of crystallography, these relations help in understanding and classifying the different crystal structures. They also have applications in computer science, where they are used in computer graphics, computer-aided design (CAD), and optimization algorithms.
Furthermore, these relations can aid in the design and fabrication of new materials with desired properties. By studying the combinatorial and geometric aspects of galxe polyhedra, researchers can gain insights into the potential applications and behavior of these materials.
In conclusion, the relations between combinatorial and geometric aspects play a crucial role in investigating the combinatorial mathematics of galxe polyhedra. They provide a deeper understanding of the structure and properties of these polyhedra and have numerous applications in various fields.
What is a galxe polyhedra?
A galxe polyhedra is a type of geometric structure that consists of a combination of regular and non-regular polygons.
What are the applications of galxe polyhedra?
Galxe polyhedra have various applications in mathematics, such as in the study of symmetry groups and topological properties of geometric structures.
How do you investigate the combinatorial mathematics of galxe polyhedra?
Investigating the combinatorial mathematics of galxe polyhedra involves studying the possible combinations of regular and non-regular polygons that can form these structures, as well as analyzing their properties and relationships.
What are some examples of galxe polyhedra?
Examples of galxe polyhedra include the rhombicuboctahedron, the snub cube, and the truncated icosidodecahedron.
Why is the study of galxe polyhedra important?
The study of galxe polyhedra is important because it helps deepen our understanding of geometric structures and their properties, and it has practical applications in various branches of mathematics and other fields such as chemistry and physics.
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
2022-2024 @ Investigating the combinatorial mathematics of galxe polyhedra
