Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
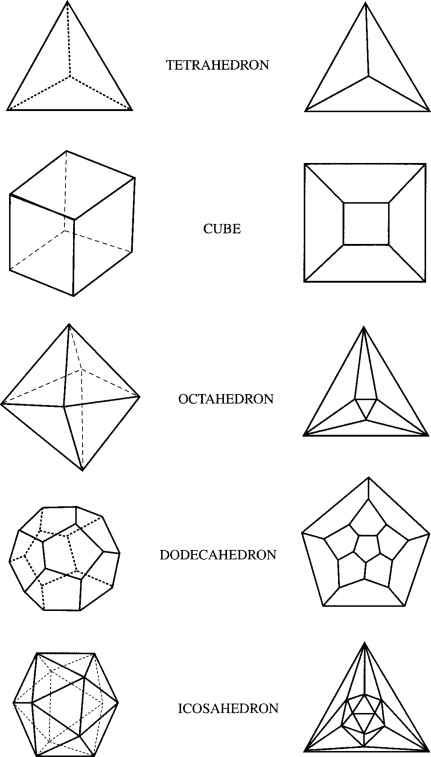
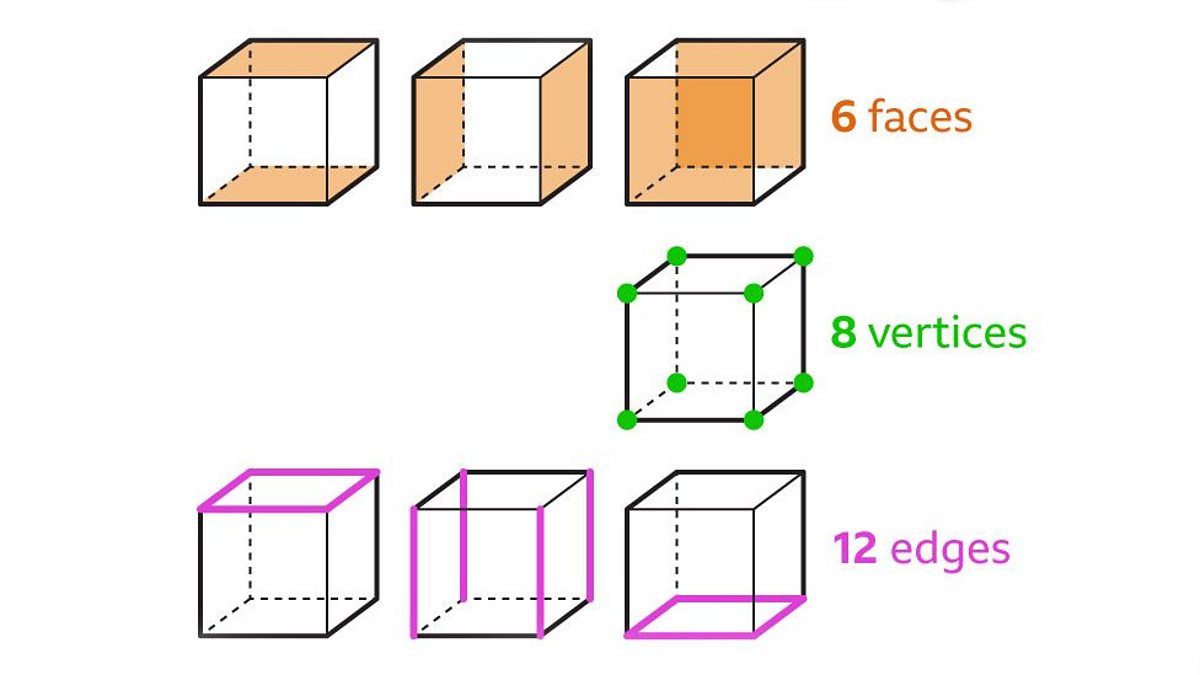
In three-dimensional space, the study of polyhedra has always fascinated mathematicians and scientists. These intricate structures, composed of multiple flat faces, edges, and vertices, are key to understanding the complexity of our world. Among the different types of polyhedra, galexe polyhedra stand out due to their unique properties.
One of the distinguishing features of galexe polyhedra is their irregularity. Unlike regular polyhedra, such as cubes or tetrahedra, galexe polyhedra do not have symmetrical faces or angles. This irregularity gives them an intriguing, almost organic quality. It is as if these polyhedra have a personality of their own, defying traditional geometric patterns.
Furthermore, galexe polyhedra possess a fascinating property known as self-duality. This means that their dual polyhedra are themselves. In other words, if you were to take the dual of a galexe polyhedron, you would end up with the original polyhedron. This self-referential nature adds another layer of complexity to their study, challenging mathematicians to explore the depths of this intriguing phenomenon.
The presence of galexe polyhedra can be observed in various fields, from crystallography to architecture. Their unique properties make them ideal for creating structures that are both aesthetically pleasing and structurally sound. Architects and designers often draw inspiration from the intricate patterns and irregular shapes of galexe polyhedra to create innovative and visually striking buildings and sculptures.
In conclusion, galexe polyhedra offer a captivating realm for exploration within the field of mathematics. Their irregularity and self-duality make them stand out among other polyhedra in three-dimensional space. As mathematicians delve deeper into their study, we can only expect to uncover more fascinating properties and applications of these enigmatic structures.
Have you ever wondered about the unique properties of galxe polyhedra in three-dimensional space? These fascinating structures have captured the attention of mathematicians and scientists alike, leading to many exciting discoveries and applications.
One of the most intriguing aspects of galxe polyhedra is their interconnected nature. Each individual polyhedron is connected to others through a network of edges and vertices, creating a complex and intricate web of connections. This interconnectedness allows for unique properties and behaviors that are not found in other geometric shapes.
The interconnected world of galxe polyhedra is a rich and diverse landscape, with countless possibilities for exploration and study. Researchers have found that these structures can exhibit emergent phenomena, where the collective behavior of the interconnected polyhedra gives rise to properties that are not seen in any individual component. This has led to applications in fields such as material science, architecture, and even computer science.
One example of the interconnected nature of galxe polyhedra can be seen in the way they can tessellate space. By connecting multiple polyhedra in specific configurations, it is possible to completely fill three-dimensional space without any gaps or overlaps. This property has been exploited in the design of efficient packing structures and has even found applications in the field of nanotechnology.
The study of galxe polyhedra and their interconnected properties is still a relatively new and rapidly evolving field. As researchers continue to explore and understand these structures, new applications and discoveries are sure to arise. If you are interested in learning more about galxe polyhedra and their interconnected world, be sure to check out the Galxe ID - Profile here.
Galxe polyhedra are three-dimensional structures with unique properties that set them apart from other geometric shapes. These polyhedra are fascinating objects of study, as their intricate design and properties have captivated mathematicians and scientists for centuries.
Galxe polyhedra are a subclass of polyhedra that have a distinct set of properties. Unlike other regular polyhedra, such as cubes or tetrahedra, galxe polyhedra have irregular faces and edges.
One of the defining characteristics of galxe polyhedra is their vertex configuration. The vertices of these polyhedra have a unique pattern, which contributes to their distinctive properties. This unique vertex arrangement gives galxe polyhedra an asymmetrical appearance, setting them apart from other polyhedra.
Galxe polyhedra exhibit several unique properties that make them intriguing subjects of study. Here are a few notable properties:
Irregular Faces: Unlike regular polyhedra, galxe polyhedra have irregular faces with varying shapes and sizes. This irregularity adds to the complexity and uniqueness of these structures.
Distinct Vertex Configuration: The vertex configuration of galxe polyhedra is different from regular polyhedra. This distinct pattern contributes to their asymmetrical appearance and sets them apart from other three-dimensional shapes.
Non-Euclidean Geometry: Galxe polyhedra can exhibit non-Euclidean geometries, which means that the rules of traditional Euclidean geometry do not apply to these structures. This adds an additional layer of complexity to their study and analysis.
Geometric Transformations: Galxe polyhedra can undergo various geometric transformations, such as rotations, translations, and reflections. These transformations can reveal different aspects of their structure and properties.
The unique properties of galxe polyhedra make them fascinating objects to explore and understand. Their irregular faces, distinct vertex configuration, non-Euclidean geometries, and geometric transformations all contribute to their allure and complexity.
By studying galxe polyhedra, mathematicians and scientists can gain a deeper understanding of the intricacies of three-dimensional space and the mathematical principles underlying these structures. Their unique properties continue to inspire new discoveries and insights in the field of geometry.
Galxe polyhedra are a fascinating and complex mathematical concept that exists in three-dimensional space. These polyhedra are unique in their properties and have been studied extensively by mathematicians and scientists.
One of the most intriguing aspects of galxe polyhedra is their intricate geometry. Unlike regular polyhedra, which have a fixed number of faces, edges, and vertices, galxe polyhedra can have a varying number of these elements. This is due to the non-uniformity of the faces, edges, and vertices of these polyhedra.
Galxe polyhedra can exhibit a wide range of geometrical properties, such as nonconvexity, self-intersecting faces, and irregularity in their shape. These properties make them challenging to study and understand, but they also make them incredibly interesting to mathematicians.
One key aspect of the geometry of galxe polyhedra is their symmetry. These polyhedra can possess various symmetry operations, such as rotational symmetry, reflection symmetry, and glide reflection symmetry. These symmetries play a crucial role in understanding the structure and characteristics of galxe polyhedra.
Another important geometrical property of galxe polyhedra is their connectivity. The way in which the faces, edges, and vertices of these polyhedra are connected determines their overall structure and shape. Understanding this connectivity is essential in analyzing and classifying galxe polyhedra.
Overall, the geometry of galxe polyhedra is a fascinating field of study that offers unique insights into the mathematical properties of three-dimensional space. By exploring the intricate geometry, symmetry, and connectivity of these polyhedra, mathematicians can gain a deeper understanding of their structure and properties, paving the way for further advancements in the field of geometry and mathematics as a whole.
The lack of conventional symmetry in galxe polyhedra arises from their unique arrangement of vertices, edges, and faces. The irregular distribution of these components results in a lack of repetitive patterns and symmetrical axes.
Instead of traditional symmetrical properties, galxe polyhedra exhibit a different form of symmetry known as self-similarity. Self-similarity is the property of an object that exhibits similar patterns or structures at different scales. In other words, galxe polyhedra possess substructures that are scaled-down versions of the whole polyhedron.
This unique form of symmetry in galxe polyhedra has significant implications in various fields, including crystallography, materials science, and architecture. The unconventional symmetry allows for the creation of complex and aesthetically appealing structures that are not bound by traditional symmetrical constraints.
Furthermore, the absence of conventional symmetry in galxe polyhedra opens up new avenues for research and exploration in the field of geometry. Scientists and mathematicians are continually discovering new properties and characteristics of galxe polyhedra that challenge our understanding of three-dimensional space.
In conclusion, the unconventional symmetry exhibited by galxe polyhedra sets them apart from regular polyhedra. Their unique arrangement of vertices, edges, and faces results in a lack of traditional symmetrical properties and the emergence of self-similarity. This unconventional symmetry has significant implications in various fields and opens up new possibilities for further exploration and study.
Galxe polyhedra are a fascinating class of three-dimensional shapes that possess unique mathematical properties. These polyhedra are formed by the intersection of planes and can be described using a set of vertices, edges, and faces. The intricate relationships between these elements create a captivating mathematical structure worth exploring.
One of the main characteristics of galxe polyhedra is their symmetry. These shapes often exhibit multiple axes of symmetry, which means that they can be rotated and reflected in ways that preserve their overall structure. This symmetry adds beauty and elegance to the polyhedra, making them visually appealing and intriguing to mathematicians and artists alike.
Another intriguing property of galxe polyhedra is their connection to other geometric shapes. By dissecting a galxe polyhedron, we can often uncover various geometric solids that fit perfectly within the structure. These solids may include cubes, tetrahedra, or even other polyhedra. This relationship between galxe polyhedra and other shapes helps to deepen our understanding of their mathematical structure.
The study of galxe polyhedra also involves exploring the relationships between their vertices, edges, and faces. Researchers have discovered various formulas and theorems that relate these elements, providing valuable insights into the unique properties of these shapes. These relationships can be represented using mathematical equations and models, allowing mathematicians to further investigate and analyze the structures of galxe polyhedra.
Furthermore, galxe polyhedra have real-world applications beyond mathematics. For example, architects and designers often draw inspiration from the intricate patterns and symmetries found in galxe polyhedra to create aesthetically pleasing buildings and structures. The study of galxe polyhedra can also have applications in physics, chemistry, and computer science, as these fields require an understanding of three-dimensional structures and their properties.
In conclusion, exploring the mathematical structure of galxe polyhedra unveils a world of fascinating properties and relationships. From their symmetries to their connections with other geometric shapes, galxe polyhedra provide an exciting area for mathematical investigation. Understanding these structures not only enriches our knowledge of mathematics but also has practical applications in various fields. Whether appreciated for their aesthetic appeal or their mathematical depth, galxe polyhedra continue to inspire and captivate researchers and enthusiasts alike.
Galxe polyhedra, with their unique geometric properties, have shown great potential in various applications within the fields of architecture and design. These polyhedra have captured the attention of architects and designers alike due to their ability to create visually striking and structurally stable structures.
One of the main applications of galxe polyhedra in architecture is the design of innovative and efficient building structures. The complex and interlocking nature of these polyhedra allows for the creation of lightweight and strong frameworks, making them ideal for the construction of large-scale buildings. These structures often exhibit great load-bearing capacities while minimizing the use of materials.
Furthermore, the intricate patterns formed by the interlocking faces of galxe polyhedra can be utilized to create unique aesthetic features in architectural designs. These structures can be used as facades, allowing for the manipulation of light and shadow to create visually captivating patterns. Additionally, the play of light on the various faces of the polyhedra can create intriguing visual effects that enhance the overall design.
Galxe polyhedra can also be used in the design of furniture and interior spaces. Their geometric shapes offer endless possibilities for creative furniture designs that are not only visually appealing but also functional. The interlocking nature of these polyhedra can contribute to the stability and durability of furniture pieces, making them suitable for contemporary and modern designs.
In addition, galxe polyhedra can be used as decorative elements in various architectural and design projects. Their unique patterns and shapes can be incorporated into wall panels, sculptures, and other art installations, adding a distinct visual element to the space. The interplay between light and the intricate surfaces of these polyhedra can create captivating experiences for viewers that engage the sense of sight.
Overall, the use of galxe polyhedra in architecture and design offers endless possibilities for innovation and creativity. From building structures to furniture design and artistic installations, these polyhedra have proven to be valuable tools for architects and designers in creating visually striking and structurally sound designs.
Galxe polyhedra have garnered significant attention in scientific research due to their unique properties and potential applications in various fields. These three-dimensional structures consist of interconnected polygons, forming a complex network that exhibits remarkable versatility.
One of the major reasons for the interest in galxe polyhedra is their ability to encapsulate other molecules or nanoparticles within their intricate framework. This property makes them ideal for drug delivery systems or as templates for the synthesis of new materials. The controlled release of these encapsulated substances can be achieved by modulating the size and shape of the polyhedra.
Furthermore, galxe polyhedra possess excellent mechanical properties, such as high stability and robustness. This makes them suitable for applications that require structural support or protection, such as in the construction of nanoscale devices or in the field of nanomedicine.
In addition to their physical properties, galxe polyhedra offer unique optical and electronic characteristics, making them suitable for optoelectronic devices and sensors. Their ability to manipulate light at the nanoscale level opens up new possibilities for advanced imaging techniques and energy harvesting systems.
Moreover, galxe polyhedra have demonstrated promising results in catalysis due to their large surface area and tunable reactivity. These structures can be tailored to provide specific sites for catalytic reactions, leading to increased efficiency and selectivity in chemical processes.
Overall, the versatility of galxe polyhedra in scientific research highlights their potential in various fields, ranging from nanotechnology to medicine. Further exploration of their properties and applications will undoubtedly lead to advancements in these areas and pave the way for innovative solutions to complex scientific challenges.
The world of galxe polyhedra is a fascinating one, with shapes and structures that defy the imagination. Found in nature, these unique geometric forms provide a window into the complexities of the universe and offer insights into the fundamental principles governing the organization of matter.
Galxe polyhedra have been observed in various natural phenomena, from the arrangement of atoms in crystals to the shapes of proteins and viruses. Their presence in nature highlights the inherent order and symmetry that underlies the formation of complex structures.
One example of galxe polyhedra in nature is the structure of carbon molecules in the form of fullerenes. These spherical polyhedra, composed of interconnected hexagons and pentagons, exhibit exceptional stability and have been found in various carbon-based materials like soot, graphite, and even in the residue of meteorite impacts.
The study of galxe polyhedra provides valuable insights into the fundamental building blocks and patterns that form the backbone of the universe. By examining these intricate structures, scientists can uncover the underlying physical laws and principles that govern the behavior of matter on both cosmic and atomic scales.
Furthermore, the unique properties of galxe polyhedra offer potential applications in various fields. Their high stability and intricate geometries can be harnessed for the development of new materials, such as superconductors or advanced catalysts. Additionally, understanding the formation and organization of galxe polyhedra can contribute to advancements in nanotechnology and the design of innovative molecular architectures.
In conclusion, galxe polyhedra in nature serve as a window into the complexities of the universe. Their presence and structures offer valuable insights into the fundamental principles governing the organization of matter and showcase the beauty of symmetry and order in the natural world.
Galxe polyhedra have captivated the scientific community with their unique properties in three-dimensional space. As researchers continue to explore the potential applications of these fascinating shapes, the future of galxe polyhedra remains full of innovative possibilities.
One exciting area of research is the development of advanced materials and structures based on galxe polyhedra. These shapes have remarkable strength-to-weight ratios, making them ideal for building lightweight yet sturdy structures. Industries such as aerospace and automotive are eager to harness the potential of galxe polyhedra to create more efficient and sustainable designs. Imagine aircraft and vehicles that are lighter, stronger, and more fuel-efficient.
Furthermore, researchers are investigating the use of galxe polyhedra in the creation of new materials with unique properties. By arranging these shapes in specific configurations, it may be possible to engineer materials with tailored properties, such as enhanced conductivity or improved energy absorption. This opens up a range of possibilities for applications in electronics, robotics, and energy storage.
The mathematical applications of galxe polyhedra are another exciting area of exploration. These shapes offer rich opportunities for studying geometric properties, symmetries, and tessellations. Mathematicians are intrigued by the challenge of classifying and analyzing galxe polyhedra, as they offer a new level of complexity compared to regular polyhedra.
Moreover, the unique properties of galxe polyhedra have the potential to revolutionize mathematical modeling and simulation. By incorporating these shapes into mathematical algorithms, researchers can create more accurate models for predicting physical phenomena, such as fluid flow, heat transfer, or even the behavior of subatomic particles.
Galxe polyhedra also have implications for the field of computational geometry, where researchers are constantly seeking efficient algorithms for solving complex geometric problems. The study of galxe polyhedra could lead to new insights and approaches for tackling these challenges.
With ongoing advancements in technology and computational power, the future of galxe polyhedra holds exciting possibilities in various domains. Whether it is in the development of advanced materials, the advancement of mathematical understanding, or the exploration of new geometric algorithms, galxe polyhedra have the potential to reshape our world in profound ways.
Disclaimer: Please note that the term "galxe polyhedra" is used fictitiously in this context for illustrative purposes.
What are galxe polyhedra?
Galxe polyhedra are three-dimensional structures composed of connected polygons, where each polygon shares an edge with at least one other polygon.
What makes galxe polyhedra unique?
Galxe polyhedra have several unique properties. Firstly, they are non-convex, meaning that they have some polygons that are bent or folded. Secondly, they have a high level of symmetry, with many rotational and reflective symmetries. Lastly, they have complex connectivity patterns, where each polygon is connected to multiple polygons.
How are galxe polyhedra different from other polyhedra?
Unlike traditional polyhedra, such as cubes or pyramids, galxe polyhedra are non-convex, meaning that they have some polygons that are bent or folded. They also have a higher level of symmetry and more complex connectivity patterns.
What are some real-life applications of galxe polyhedra?
Galxe polyhedra have several potential real-life applications. They can be used in computer graphics and animation to create complex and visually interesting shapes. They can also be used in materials science to study the properties of novel materials with non-convex structures. Additionally, they can be used in architectural design to create unique and aesthetically pleasing structures.
What is the significance of studying galxe polyhedra?
Studying galxe polyhedra is significant for several reasons. Firstly, they provide insights into the properties and behavior of complex three-dimensional structures. Secondly, they have practical applications in various fields, such as computer graphics, materials science, and architecture. Lastly, they inspire creativity and innovation by challenging traditional notions of geometric shapes and structures.
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
2022-2024 @ The unique properties of galxe polyhedra in three dimensional space
