Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
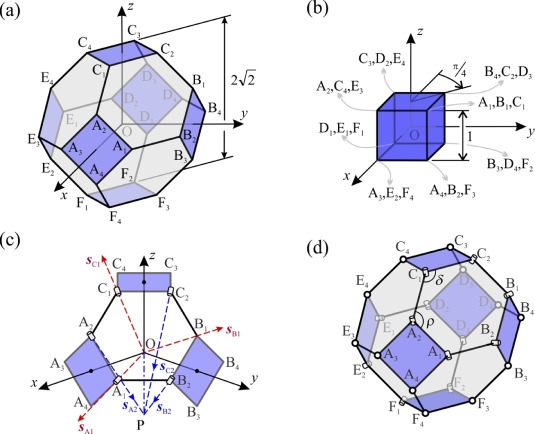
Galaxy polyhedra, also known as stellated polyhedra, are fascinating geometric shapes that are composed of interconnected polygons. These complex structures resemble celestial bodies and offer a multitude of intriguing transformations that can be applied to them. By understanding the principles behind these geometric transformations, we can gain insight into the intricacies of the universe and explore the beauty of mathematics.
Geometric transformations play a vital role in the field of mathematics and have wide-ranging applications in various disciplines, including computer graphics, physics, and architecture. By manipulating the vertices, edges, and faces of a galaxy polyhedron, we can explore the effects of transformations such as translation, rotation, and scaling. These transformations allow us to observe how the polyhedron changes in shape, size, and orientation while preserving its underlying structure.
One of the fundamental geometric transformations applied to galaxy polyhedra is the dilation or scaling transformation. By stretching or shrinking the polyhedron in relation to a fixed center or point, we can visualize the effect of changing its size. This transformation not only changes the overall dimensions of the polyhedron, but also affects the proportions and distances between its vertices, edges, and faces. Understanding the behavior of galaxy polyhedra under scaling transformations helps us gain insights into the concept of similarity and the scale invariance of geometric objects.
Another captivating geometric transformation of galaxy polyhedra is rotation. By rotating the polyhedron around a fixed axis or point, we can observe the change in its orientation in space. This transformation enables us to explore the symmetries and asymmetries of the polyhedron and reveals its hidden patterns. By studying the rotational properties of galaxy polyhedra, we can uncover the concept of rotational symmetry, which plays a significant role in the study of crystallography, as well as bring an aesthetic appeal to architectural designs.
In conclusion, the study of geometric transformations of galaxy polyhedra allows us to delve into the mysteries of the universe and the wonders of mathematics. By understanding how these complex structures change under translations, rotations, and scalings, we gain valuable insights into the underlying principles of geometry. The intricate interplay of shape, size, and orientation in galaxy polyhedra not only offers a visual delight, but also opens new avenues for exploration and discovery in various scientific fields.
Geometric transformations are fundamental concepts in the field of mathematics that involve altering the size, position, or shape of an object. These transformations play a crucial role in various areas, such as computer graphics, architecture, and physics. In the context of galxe polyhedra, understanding geometric transformations is essential for analyzing and studying their properties.
There are several types of geometric transformations that can be applied to galxe polyhedra:
Translation is a type of transformation that moves an object from one position to another without changing its shape or size. In the context of galxe polyhedra, translation involves shifting the entire polyhedron in a specific direction without altering its internal structure.
Rotation is a transformation that involves turning an object around a fixed point called the center of rotation. In the case of galxe polyhedra, rotation can be used to change the orientation or position of the polyhedron without changing its shape or size.
Understanding the basics of geometric transformations is crucial for exploring the properties and behavior of galxe polyhedra. By applying different transformations, mathematicians can analyze the effects of these changes on the polyhedra and discover new insights.
If you are interested in learning more about galxe polyhedra and their geometric transformations, you can visit Galxe ID - Profile. This platform provides comprehensive resources and tools for exploring and studying galxe polyhedra in depth.
Geometric transformations are crucial in the field of mathematics, particularly when studying galactic polyhedra. These transformations help us understand the relationship between different shapes, how they change under certain operations, and how they can be visualized in three-dimensional space. They provide a powerful tool for exploring and analyzing the intricate structures of galactic polyhedra.
Geometric transformations allow us to visualize complex structures of galactic polyhedra in a more comprehensible way. By applying transformations such as rotations, translations, and reflections, we can simplify the visualization of intricate shapes and understand their symmetries and patterns. This helps us identify common characteristics among different polyhedra and classify them into distinct groups.
Understanding geometric transformations enables us to predict how galactic polyhedra behave under different operations. For example, by applying rotation transformation to a polyhedron, we can predict how its vertices, edges, and faces will change. This knowledge is crucial in fields such as architecture, engineering, and computer graphics, where predicting changes in the shape of objects is essential.
Furthermore, geometric transformations help us study the stability and energy levels of galactic polyhedra. By analyzing the transformation matrices, we can understand the effects of different transformations on the polyhedra's stability and energy. This knowledge is valuable in fields like chemistry and material science, where the stability and properties of polyhedral structures are of great importance.
Studying geometric transformations of galactic polyhedra often leads to the development of new mathematical concepts. These concepts can be applied not only to the study of polyhedra but also to various other branches of mathematics. For example, the understanding of transformations can provide insights into the study of symmetry groups, topological properties, and even abstract algebra.
1. Simplifying visualization of complex structures
2. Predicting behavioral changes
3. Developing new mathematical concepts
In conclusion, understanding geometric transformations is crucial for comprehending the intricate structures of galactic polyhedra. It allows us to visualize complex shapes, predict behavioral changes, and even contribute to the development of new mathematical concepts. By studying these transformations, we gain a deeper understanding of the fundamental principles that govern the geometrical world and its applications in various fields.
Galxe polyhedra are a fascinating subject that offers a unique opportunity to delve into the world of geometric transformations. These polyhedra, also referred to as stellated polyhedra, are three-dimensional structures formed by extending the faces or edges of a platonic solid.
One of the most intriguing aspects of Galxe polyhedra is their ability to exhibit symmetries that are not present in the original platonic solid. By extending the faces or edges, new vertices are created, and these new vertices can be connected to form additional faces. This process can be repeated multiple times to generate complex, symmetrical structures.
Exploring Galxe polyhedra allows us to study the effects of these transformations on the properties of the original platonic solid. For example, the number of vertices, edges, and faces may increase or decrease, and the resulting polyhedra can have different degrees of symmetry compared to the original solid.
Through careful analysis and visualization, we can gain insights into the underlying mathematical principles behind these transformations. We can also explore the geometrical properties and relationships between the different components of the Galxe polyhedra.
The study of Galxe polyhedra has applications in various fields, including architecture, art, and computer graphics. Architects and designers often incorporate the unique symmetries and striking visual patterns of Galxe polyhedra in their work, creating visually stunning structures and sculptures.
Galxe polyhedra can also be employed in computer graphics to generate complex 3D models with intricate geometries. These models can be used in video games, animation, and virtual reality applications to enhance the visual experience and create realistic virtual environments.
With advancements in computational power and visualization techniques, we can expect further advancements in the exploration of Galxe polyhedra. Researchers and mathematicians will continue to uncover new patterns, symmetries, and transformations, expanding our understanding of these intriguing structures.
As our knowledge of Galxe polyhedra grows, so too does our ability to apply them in various fields. The exploration of Galxe polyhedra not only provides new insights into geometry and mathematics but also opens up opportunities for artistic, architectural, and technological innovation.
Geometric transformations are fundamental operations that modify the shape, size, or position of geometric objects. Understanding these transformations is essential for analyzing and manipulating galxe polyhedra, which are three-dimensional shapes composed of regular polygons.
Translation is a transformation that moves an object from one position to another without changing its shape or orientation. It involves shifting all the points of the object by a fixed distance in a specified direction. In galxe polyhedra, translation can be used to create symmetrical patterns by repeating a specific translation multiple times.
Rotation is a transformation that turns an object around a fixed point called the center of rotation. It involves rotating all the points of the object by a specified angle and direction. In galxe polyhedra, rotation can be used to create new shapes and explore rotational symmetry, where an object remains unchanged after one or more rotations.
These common types of geometric transformations are the building blocks for understanding and analyzing the geometrical properties of galxe polyhedra. By applying these transformations, mathematicians and researchers can uncover fascinating patterns and relationships within these complex three-dimensional shapes.
Geometric transformations, such as translations, rotations, and reflections, play a crucial role in understanding the properties of galxe polyhedra. These transformations allow us to manipulate and analyze the shapes of these fascinating three-dimensional structures.
Translations involve moving every point of a galxe polyhedron by a fixed distance in a specified direction. By applying translations, we can shift the entire polyhedron in space without changing its orientation or shape.
Rotations are transformations that involve rotating a galxe polyhedron around a fixed axis. The polyhedron remains the same shape, but its orientation changes. By specifying the angle and axis of rotation, we can perform various rotations and explore different perspectives of the polyhedron.
Reflections are transformations that involve flipping a galxe polyhedron across a plane. This transformation changes the orientation of the polyhedron, but not its shape. Through reflections, we can study the symmetries and mirror images of the polyhedron.
By applying these geometric transformations to galxe polyhedra, we can gain insights into their symmetries, rotational properties, and relationship to other three-dimensional shapes. These transformations allow us to explore the geometric features and characteristics of these complex structures, paving the way for further advancements in mathematical and scientific research.
Geometric transformations are essential concepts in the field of mathematics and play a significant role in understanding the properties of galaxe polyhedra. By applying various transformations, such as translation, rotation, and dilation, we can visually explore how these polyhedra can be manipulated and changed.
In this article, we will demonstrate geometric transformations using examples that showcase the effects of different transformations on galaxe polyhedra. These examples will serve as visual aids, allowing readers to better grasp the concept and intuition behind each transformation.
Translation
A translation moves an object from one position to another without changing its shape or orientation. It involves shifting the entire object along a given vector.
Rotation
A rotation involves rotating an object around a fixed point called the center of rotation. It changes the orientation of the object while preserving its shape.
Dilation
A dilation involves scaling an object up or down by multiplying its coordinates by a scalar factor. It changes the size of the object while preserving its shape.
Through these examples, readers will develop a deeper understanding of how these transformations affect the geometry of galaxe polyhedra. By visually witnessing the changes in shape, size, and orientation, readers will be able to comprehend the fundamental principles behind geometric transformations and apply them to a wide range of mathematical problems and concepts.
Geometric transformations play a crucial role in understanding the intricate structure of galactic polyhedra. They represent the changes that occur when shapes are moved, rotated, reflected, or scaled in space. While these transformations offer a deeper insight into the properties and relationships between different polyhedral forms, they present some significant challenges in their comprehension.
One of the main challenges lies in visualizing and mentally manipulating these geometric transformations. As humans, we tend to think in three-dimensional terms, which can become complex when dealing with higher-dimensional objects or transformations. Visualizing these changes becomes even trickier when considering the dynamic nature of polyhedra and their transformations.
Furthermore, understanding the mathematical representation and notation of geometric transformations can be quite challenging. Different notations, such as matrix or vector representations, may be used depending on the specific transformation and its application. Deciphering and interpreting these notations correctly is essential for accurately understanding and applying geometric transformations.
Another challenge involves comprehending the effects of combining multiple transformations. When several transformations are applied sequentially or simultaneously, their individual effects can interact and potentially create unexpected outcomes. Analyzing and predicting these consequences require a deep understanding of the underlying mathematical principles and properties.
Additionally, the study of geometric transformations requires a solid foundation in mathematical concepts and principles. Understanding the underlying geometry and spatial relationships is crucial for making sense of the transformations. Lack of familiarity with these fundamentals can pose a significant challenge in fully grasping the intricacies and nuances of geometric transformations.
In conclusion, comprehending geometric transformations in the context of galactic polyhedra presents several challenges. Overcoming the difficulties in visualizing, understanding mathematical representations, interpreting combined transformations, and acquiring a strong mathematical foundation are crucial for gaining a comprehensive understanding of these intricate structures.
What are geometric transformations of galxe polyhedra?
Geometric transformations of galxe polyhedra refer to the various ways in which these three-dimensional figures can be changed or manipulated. These transformations include rotations, translations, and reflections.
Why are geometric transformations important in understanding galxe polyhedra?
Geometric transformations are important in understanding galxe polyhedra because they allow us to visualize how these figures can be altered in space. By applying transformations, we can study the properties and relationships between different polyhedra.
How do rotations affect galxe polyhedra?
Rotations can change the orientation of galxe polyhedra in space. A rotation involves turning the polyhedron around a fixed point called the center of rotation. This transformation preserves the shape and size of the figure but can change its position in three-dimensional space.
What happens to the shape of a galxe polyhedron during a reflection?
During a reflection, the shape of a galxe polyhedron remains the same, but it is flipped across a line called the axis of reflection. This transformation creates a mirror image of the original figure. The size and orientation of the polyhedron are preserved.
Can translations transform one galxe polyhedron into another?
No, translations cannot transform one galxe polyhedron into another. Translations involve moving the entire polyhedron without changing its shape, size, or orientation. To transform one polyhedron into another, you would need to apply other geometric transformations such as rotations or reflections.
What are geometric transformations of polyhedra?
Geometric transformations of polyhedra are changes in the shape, position, or orientation of a polyhedron. These transformations can include translations, rotations, reflections, and dilations.
How do geometric transformations affect the properties of polyhedra?
Geometric transformations can change the size, shape, and orientation of a polyhedron, but they do not change its fundamental properties such as the number of faces, edges, and vertices.
What is the difference between translations and rotations?
Translations involve moving a polyhedron without changing its shape or orientation, while rotations involve spinning a polyhedron around a fixed point. Translations can be thought of as "slides" and rotations as "spins".
Can geometric transformations be applied to three-dimensional objects other than polyhedra?
Yes, geometric transformations can be applied to any three-dimensional object, not just polyhedra. They are a fundamental concept in geometry and are used to study and analyze objects in space.
What is the practical application of understanding geometric transformations of polyhedra?
Understanding geometric transformations of polyhedra has practical applications in fields such as architecture, computer graphics, and engineering. It allows for efficient design and analysis of three-dimensional structures and objects.
Galxe login | Galxe ID | Passport | Explore Campaigns | Galxe products
2022-2024 @ Understanding geometric transformations of galxe polyhedra
